We are often reliant on GPS co-ordinates being delivered to our devices for locating places. With a little practice it’s not hard to read a decimal latitude and longitude value to determine a rough position.
But first it’s important to understand some key concepts.
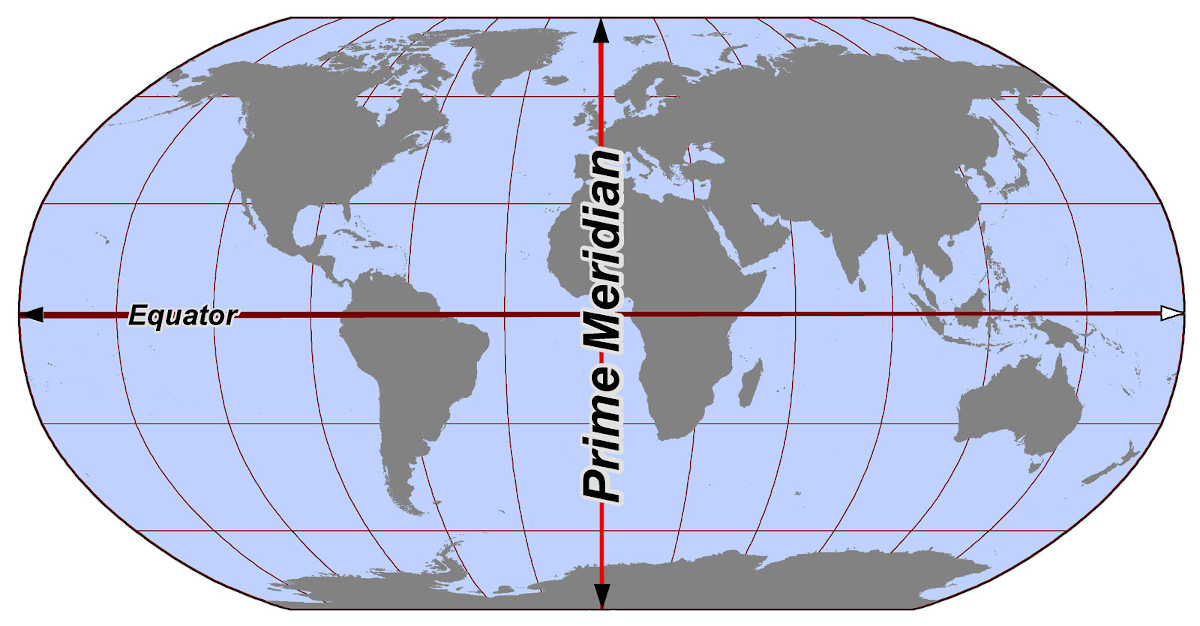
The Prime Meridian divides the globe into Eastern and Western hemispheres, just as the equator divides the globe into Northern and Southern hemispheres. In the diagram above:
- Top right quadrant: Northern latitudes, Eastern longitudes
- Bottom right quadrant: Southern latitudes, Eastern longitudes
- Bottom left quadrant: Southern latitudes, Western longitudes
- Top left quadrant: Northern latitudes, Western longitudes
The Prime Meridian is at 0 degrees longitude (neither East or West), just as the equator is at 0 degrees latitude (neither North or South).
The spot south of Ghana where the Prime Median and Equator intersect has the co-ordinates 0 degrees latitude and 0 degrees longitude.
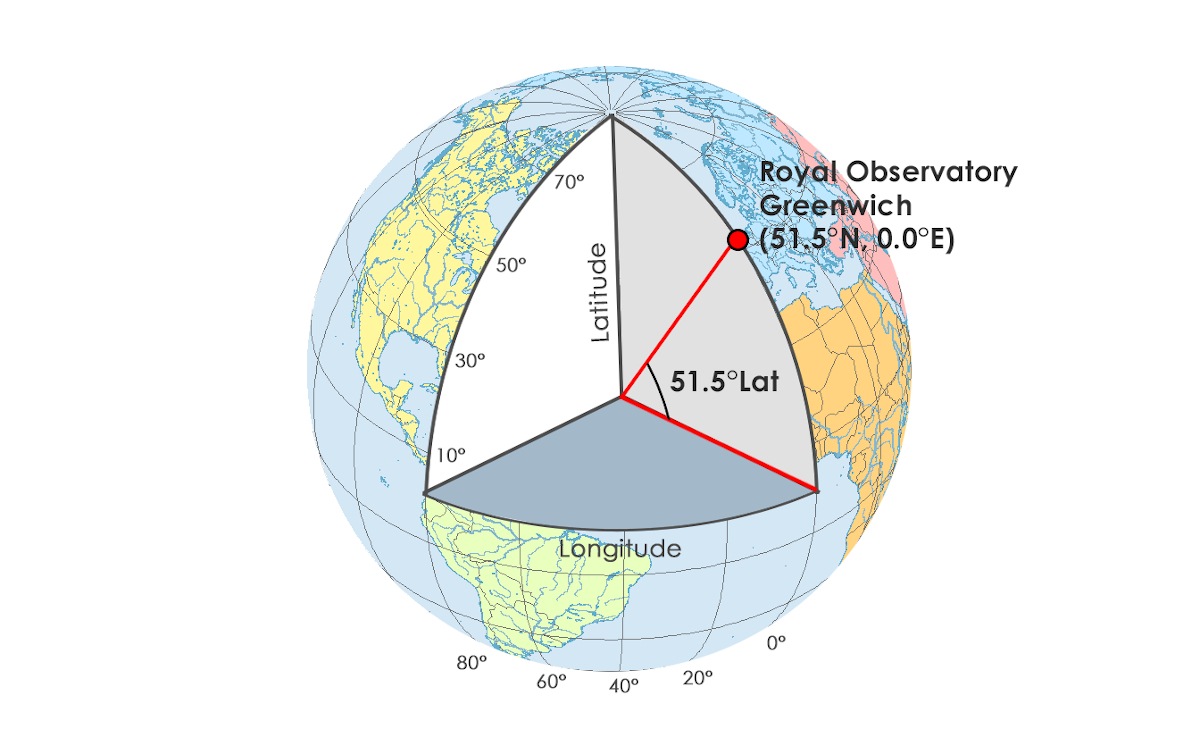
To help understand where degrees come from, imagine there is an imaginary point in the center of the Earth. You are standing on it, facing Greenwich in London.
By facing the Prime Meridian line, you are facing 0 degrees longitude (neither East nor West). Now you need to look up to face Greenwich. It is that angle (the angle you need to look up by to face London) that represents its latitude, which is 51.5 degrees (North).
Let’s now look to the other side of the world… almost… to Sydney, Australia. This time you need to turn to your left (East) by 151.2093 degrees (longitude) and look down (South) by 33.8688 degrees (latitude).
Although it’s a little more abstract to visualise, you can turn a maximum of 180 degrees from the prime meridian (either East or West) and 90 degrees from the equator (North or South). Using a mix of the two, you will be facing some point on the earth from your imaginary point in the center.
Above, I reported Sydney as 33.8688° S (latitude), 151.2093° E (longitude).
You could have previously seen latitude and longitude positions reported with negative values (e.g. -33.8688,151.2093). This format is referred to as Decimal Degrees (DD) and is the most common format used today. It’s still in latitude,longitude format, but now instead of using North or South for latitude, and East and West for longitude, +/- values are used.
Northern latitudes and Eastern longitudes are positive. Southern latitudes and Western longitudes are negative.
Here are some example of cities in each of the quadrants and their latitudes and longitudes reported in the two ways described above:
- Top right quadrant: Northern latitudes, Eastern longitudes
- e.g. Moscow = 55.7558° N, 37.6173° E (55.7558,37.6173)
- Bottom right quadrant: Southern latitudes, Eastern longitudes
- e.g. Sydney = 33.8688° S, 151.2093° E (-33.8688,151.2093)
- Bottom left quadrant: Southern latitudes, Western longitudes
- e.g. Sao Paulo = 23.5558° S, 46.6396° W (-23.5558,-46.6396)
- Top left quadrant: Northern latitudes, Western longitudes
- e.g San Francisco = 37.7749° N, 122.4194° W (37.7749,-122.4194)
You might have come across other systems reporting latitude and longitude including; Degrees, Minutes, and Seconds (DMS) – the oldest format for geographic coordinates (though still used extensively today (including in camera metadata).
For example, here’s a snippet of the metadata from a GoPro 360 photo reporting latitude and longitude in DMS:
<Composite:GPSAltitude>2323.6 m Above Sea Level</Composite:GPSAltitude>
<Composite:GPSDateTime>2019:11:29 13:06:48Z</Composite:GPSDateTime>
<Composite:GPSLatitude>28 deg 17' 55.14" N</Composite:GPSLatitude>
<Composite:GPSLongitude>16 deg 32' 44.90" W</Composite:GPSLongitude>
<Composite:GPSPosition>28 deg 17' 55.14" N, 16 deg 32' 44.90" W</Composite:GPSPosition>
You can see (after converting ASCII characters) the location reads 28 deg 17’ 55.14” North (latitude) and 16 deg 32’ 44.90” West (longitude).
Breaking it down we have:
- 28 deg 17’ 55.14” North (latitude)
- 28 degrees
- 17 minutes
- 55.14 seconds
- North
- 16 deg 32’ 44.90” West (longitude)
- 16 degrees
- 32 minutes
- 44.90 seconds
- West
Degrees reported here are no different to the way previously described.
Minutes and seconds are where it gets tricky.
Let’s start with latitude. Try and imagine lines circling the globe in Northern latitudes from the equator to the North Pole each 1 degree apart.
In globe image above, you can see some of these lines circling the globe representing 10°, 30°, 50°, 70° latitude.
Between each of these degrees, there are 60 minutes (or 60 more lines), and between each minute is 60 seconds (or 60 minutes).
Degrees for latitude range from 0-90, minutes between 0 to 59 as integers and seconds between 0 to 59.9999 (reported up to 8 decimal places – see note on accuracy below) with North or South value reported.
The same system is in place for latitude, the only difference being degrees range 0-180 with East or West values reported.
Converting to Decimal Degrees from Degrees, Minutes, and Seconds we can use the following equation
DD = d + m/60 + s/3600
So in my GoPro example (28 deg 17' 55.14" North, 16 deg 32' 44.90" West)
DD = d + m/60 + s/3600
lat DD = (28 + (17/60) + (55.14/3600)) * 1
lat DD = 28.29865
(North, but if south * by -1)
lon DD = (16 + (32/60) + (44.90/3600)) * -1
lon DD = -16.5458055556
(West, so * by -1)
Which gives us a DD latitude,longitude = 28.29865,-16.5458055556.
A note on accuracy
The number of decimal places reported in the latitude and longitude values is important, as it determines the precision of the location.
In a world without computers decimal places were a major consideration. As computerised GPS systems entered the market this became less of a concern because computers can now easily report location to many decimal places from GPS readings.
The biggest issue with GPS accuracy today is down to the device and conditions.
A device might report to 8 decimal places (good for millimeter level accuracy), but if the measurement calculated by the GPS receiver based on satellite fixes is inaccurate then the measurement will be reported to a high degree of accuracy, but is in fact not very accurate at all (see GPS 101 for causes of inaccuracy).
Never miss an update
Sign up to receive new articles in your inbox as they published.
Discuss this post
